fredag 29 april 2011

Viktat Glidande Medelvärde

Ett viktat glidande medelvärde (WMA) skiljer sig från ett enkelt glidande medelvärde (SMA) i det att varje dag som ska observeras inte ges samma vikt. Istället avtar vikten linjärt ju äldre priset är.
Detta har fördelen att medelvärdet reagerar snabbare på nyare prisförändringar (dock med störning). Formeln för WMA ser ut så här (taget från Wikipedia):
\text{WMA}_{M} = { n p_{M} + (n-1) p_{M-1} + \cdots + 2 p_{(M-n+2)} + p_{(M-n+1)} \over n + (n-1) + \cdots + 2 + 1}


N är antalet dagar medelvärdet är inställt på och vi ser att täljaren är en aritmetisk talföljd, vilket då kan representeras av en aritmetisk summaformel (du kommer väl ihåg matte c?).

Så här skulle viktfördelningen se ut för n = 15.



Till skillnad från det mer populära exponentiellt viktade medelvärdet (EMA) så finns det inget evigt minne, utan värde kan beräknas exakt från en dag i taget. För att göra det behöver man dock en funktion som kan hantera additionen, speciellt när det handlar om många vikter. En funktion i VBA kommer att ges i kommentatorfältet.


KvA
Upplagd av kl.
Etiketter:

1 kommentar:

  1. Kvantitativ Analys29 april 2011 kl. 00:34

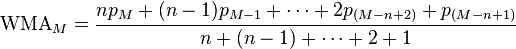
    Function WMA(Cell As Range, Längd As Double)

    'Linjärt viktat glidande medelvärde
    'Av www.kvantitativ-analys.blogspot.com
    'Längd = Antal dagar för på vilka värdet ska beräknas


    y = Cell.Row
    x = Cell.Column
    Summa = (Längd * (1 + Längd)) / 2

    yy = Längd

    For i = 1 To yy
    WMA = Cells(i - Längd + y, x).Value * (i / Summa) + WMA
    Next i


    End Function

    SvaraRadera

Prenumerera på: Kommentarer till inlägget (Atom)